Machine-learning-based spatio-temporal super resolution reconstruction of turbulent flows
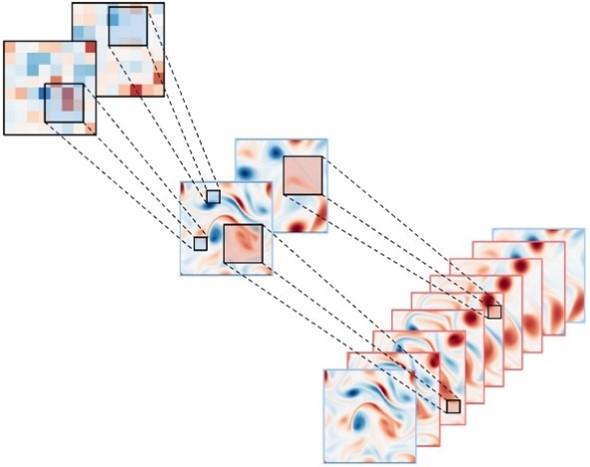
Title: Machine-learning-based spatio-temporal super resolution reconstruction of turbulent flows
Authors: Kai Fukami, Koji Fukagata and Kunihiko Taira
Journal: Journal of Fluid Mechanics, Vol: 909, A9 (2021)
DOI: 10.1017/jfm.2020.948
Abstract:
We present a new data reconstruction method with supervised machine learning techniques inspired by super resolution and inbetweening to recover high-resolution turbulent flows from grossly coarse flow data in space and time. For the present machine-learning-based data reconstruction, we use the downsampled skip-connection/multiscale model based on a convolutional neural network, incorporating the multiscale nature of fluid flows into its network structure. As an initial example, the model is applied to the two-dimensional cylinder wake at ReD=100. The reconstructed flow fields by the present method show great agreement with the reference data obtained by direct numerical simulation. Next, we apply the current model to a two-dimensional decaying homogeneous isotropic turbulence. The machine-learned model is able to track the decaying evolution from spatial and temporal coarse input data. The proposed concept is further applied to a complex turbulent channel flow over a three-dimensional domain at Reτ=180. The present model reconstructs high-resolved turbulent flows from very coarse input data in space, and also reproduces the temporal evolution for appropriately chosen time interval. The dependence on the number of training snapshots and duration between the first and last frames based on a temporal two-point correlation coefficient are also assessed to reveal the capability and robustness of spatio-temporal super resolution reconstruction. These results suggest that the present method can perform a range of flow reconstructions in support of computational and experimental efforts.
Related Articles:
- Super-resolution reconstruction of turbulent flows with machine learning Journal of Fluid Mechanics, Vol. 870, pp. 106-120 (2019). DOI: 10.1017/jfm.2019.238.
- Assessment of supervised machine learning methods for fluid flows . Theoretical and Computational Fluid Dynamics, Vol. 34, pp. 497-519 (2020). DOI: 10.1007/s00162-020-00518-y.
- Global field reconstruction from sparse sensors with Voronoi tessellation-assisted deep learning. Nature Machine Intelligence, Vol. 3, pp. 945-951 (2021). DOI: 10.1038/s42256-021-00402-2.





